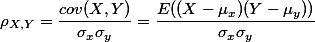霍普金斯统计量原理
在给数据集做聚类之前,我们需要事先评估数据集的聚类趋势,要求数据是非均匀分布,均匀分布的数据集没有聚类的意义。
霍普金斯统计量是一种空间统计量,用于检验空间分布的变量的空间随机性,从而判断数据是否可以聚类。
计算步骤:
-
均匀地从D的空间中抽取n个点p1,p2,…pn,对每个点pi(1≤i≤n),找出pi在D中的最近邻,并令xi为pi与它在D中的最近邻之间的距离,即
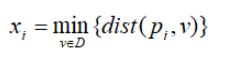
-
均匀地从D的空间中抽取n个点q1,q2,…qn,对每个点qi(1≤i≤n),找出qi在D-{qi}中的最近邻,并令yi为qi与它在D-{qi}中的最近邻之间的距离,即
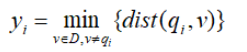
-
计算霍普金斯统计量H
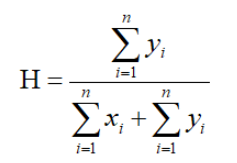
如果样本接近随机分布,H的值接近于0.5;如果聚类趋势明显,则随机生成的样本点距离应该远大于实际样本点的距离,即H的值接近于1

具体可见:https://www.datanovia.com/en/lessons/assessing-clustering-tendency/#statistical-methods
Python实现
from sklearn.neighbors import NearestNeighbors
from random import sample
import numpy as np
import pandas as pd
from numpy.random imort uniform
def hopkins_statistic(x):
d = x.shape[1]
n = len(x)
m = int(0.1*n)
nbrs = NearestNeighbors(n_neighbors=1).fit(x.values)
rand_x = sample(range(0,n),m)
ujd = []
wjd = []
for j in range(0,m):
u_dist, _ = nbrs.kneighbors(uniform(np.min(x,axis=0), np.max(x, axis=0), d).reshape(1,-1), 2 , return_distince=True)
ujd.append(u_dist[0][1])
w_dist, _ = nbrs.kneighbors(x.iloc[rand_x[j]].values.reshape(1, -1), 2, return_distince=True)
wjd.append(w_dist[0][1])
h = sum(ujd)/(sum(ujd)+sum(wjd))
if isnan(h):
print(ujd, wjd)
h = 0
return h